Deep Residual Learning for Image Recognition

Abstract

**p **: 深的卷积神经网络很难训练

K: 使用残差学习的框架 , 使得深的卷积神经网络容易训练

S: 层作为一个学习残差函数相对于层输入的一个方法，而不是一个unreferenced fuctions 的方式

E: ImageNet 数据集上使用了152层深度，相较于VGG深8倍，计算复杂度要低，COCO28%相关改进，仅替换为残差学习

Introduction

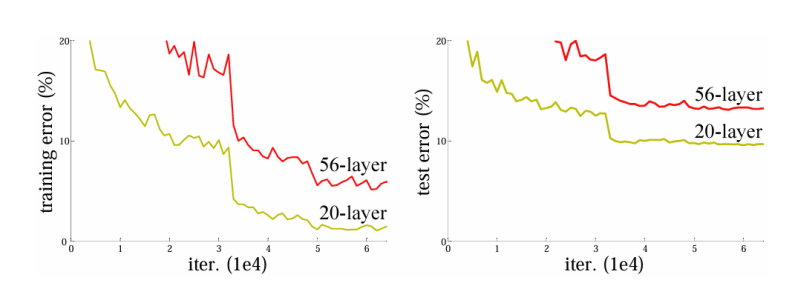
一般在第一页右上角放上一张最好看的图，扩展：prof. Randy —CMU最后一课

更深的神经网络随着训练轮数增加训练误差反而会变得更高，测试误差也会更高

网络堆叠的过于深的话，梯度会出现爆炸或者消失

传统解决办法：

在权重随机初始化的时候，设定好权重的大小，并在中间加入 normalization , 校验每个层的输出和它的梯度的均值和方差，避免有一些曾过大或者某一些层过小，保证能够收敛。

问题：

浅的网络效果不错的话，加一些层深的网络不应该变差，这些加入的深的层理论上相当于 identify mapping ,。

过拟合(overfiitting) ：在一个数据集上，训练误差变低，测试误差增加

identify mapping: f(x) = x , 输入 x ，输出 x , 等价于权重训练成简单的 1/n

提出的全新方法：

Deep Residual learning framework（residual connection）

新加的层：F(X) := H（x）- x 输出： F(X) + X

思想：浅的层输出的东西，不直接拿来学，而是学新的层学到的东西与真实的东西的残差 H（x）-x，输出的为F(x)+x ,简单来说你的输出等于你的输出加上你的输入

alt

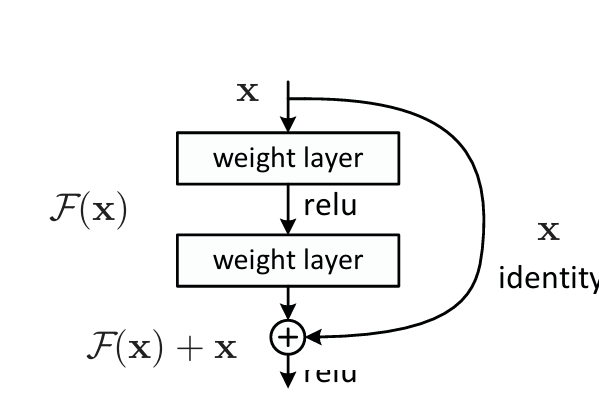
F(X) + X 的实现通过 shortcut connections 实现，不会增加任何要学的参数，也不会让计算变复杂。

# 残差块结构（假设输入x的通道数为64）
x_input = x  # 原始输入
x = Conv2D(64, kernel_size=3, padding='same')(x)
x = BatchNorm()(x)
x = ReLU()(x)
x = Conv2D(64, kernel_size=3, padding='same')(x)
x = BatchNorm()(x)
F_x = x  # F(x) 是经过两次卷积、批归一化和激活后的结果
H_x = F_x + x_input  # 最终输出 = F(x) + x
H_x = ReLU(H_x)      # 最后再经过一次激活

residual 早年在机器学习中提出过了，早期线性模型的解法是靠residual不断迭代的。

思路：很多经典paper其实都是前人提出的方法巧妙地进行结合，迁移运用解决当前热门难题

Abstract

Introduction

related work